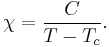Curie temperature
In physics and materials science, the Curie temperature (Tc), or Curie point, is the temperature at which a ferromagnetic or a ferrimagnetic material becomes paramagnetic on heating; the effect is reversible. A magnet will lose its magnetism if heated above the Curie temperature. The term is also used in piezoelectric materials to refer to the temperature at which spontaneous polarization is lost on heating. An analogous temperature, the Néel temperature, is defined for antiferromagnetic materials. The Curie temperature is named after Pierre Curie.
Below the Curie temperature neighboring magnetic spins are aligned parallel within in ferromagnetic materials and anti-parallel in ferrimagnetic materials. As the temperature is increased towards the Curie point, the alignment (magnetization) within each domain decreases. Above the Curie temperature, the material is paramagnetic so that magnetic moments are in a completely disordered state.
The destruction of magnetization at the Curie temperature is a second-order phase transition and a critical point where the magnetic susceptibility is theoretically infinite.
A heat-induced ferromagnetic-paramagnetic transition is used in magneto-optical storage media, for erasing and writing of new data. Famous examples include the Sony Minidisc format, as well as the now-obsolete CD-MO format. Other uses include temperature control in soldering irons, and stabilizing the magnetic field of tachometer generators against temperature variation.[1]
Contents |
Curie temperature in ferromagnetic and ferrimagnetic materials
Given below are various Curie temperatures for different substances.[2]
| Substance | Curie temp °C |
|---|---|
| Iron (Fe) | 770 |
| Cobalt (Co) | 1130 |
| Nickel (Ni) | 358 |
| Iron Oxide (Fe2O3) | 622 |
Gadolinium is ferromagnetic at temperatures below 19 °C (66 °F)[3], approximately room temperature, and strongly paramagnetic above that temperature.
Curie temperature in piezoelectric materials
In analogy to ferromagnetic materials, the Curie temperature is also used in piezoelectric materials to describe the temperature above which the material loses its spontaneous polarization and piezoelectric characteristics. In lead zirconate titanate (PZT), the material is tetragonal below Tc and the unit cell contains a displaced central cation and hence a net dipole moment. Above Tc, the material is cubic and the central cation is no longer displaced from the centre of the unit cell. Hence, there is no net dipole moment and no spontaneous polarization.
The Curie-Weiss law
A simple theory predicts that, above the Curie temperature, the magnetic susceptibility, χ, is given by the Curie-Weiss law:
where C is a material-specific Curie constant, T is absolute temperature, measured in kelvins, and Tc is the Curie temperature, measured in kelvins.
Thus, the susceptibility approaches infinity as the temperature approaches Tc.[4]
See also
Notes
- ^ Pallàs-Areny & Webster 2001, pp. 262–263
- ^ Buschow 2001, page 5021, table 1
- ^ The Elements, Theodore Gray, Black Dog & Leventhal Publishers, 2009
- ^ Kittel 1986
References
- Buschow, K. H. J. (2001). Encyclopedia of materials : science and technology. Elsevier. ISBN 0-08-043152-6.
- Kittel, Charles (1986). Introduction to Solid State Physics (sixth ed.). John Wiley & Sons. ISBN 0-471-87474-4.
- Pallàs-Areny, Ramon; Webster, John G (2001). Sensors and Signal Conditioning (2nd ed.). John Wiley & Sons. pp. 262–263. ISBN 978-0-471-33232-9.
External links
- Ferromagnetic Curie Point. Video by Walter Lewin, M.I.T.